Prev Tutorial: Extract horizontal and vertical lines by using morphological operations
Next Tutorial: Basic Thresholding Operations
In this tutorial you will learn how to:
Imagine the pyramid as a set of layers in which the higher the layer, the smaller the size.
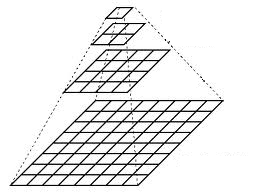
To produce layer \((i+1)\) in the Gaussian pyramid, we do the following:
\[\frac{1}{16} \begin{bmatrix} 1 & 4 & 6 & 4 & 1 \\ 4 & 16 & 24 & 16 & 4 \\ 6 & 24 & 36 & 24 & 6 \\ 4 & 16 & 24 & 16 & 4 \\ 1 & 4 & 6 & 4 & 1 \end{bmatrix}\]
This tutorial code's is shown lines below.
Let's check the general structure of the program:
Perform an infinite loop waiting for user input. Our program exits if the user presses ESC. Besides, it has two options:
Perform upsampling - Zoom 'i'n (after pressing 'i')
We use the function pyrUp() with three arguments:
Perform downsampling - Zoom 'o'ut (after pressing 'o')
We use the function pyrDown() with three arguments (similarly to pyrUp()):
Notice that it is important that the input image can be divided by a factor of two (in both dimensions). Otherwise, an error will be shown.
The program calls by default an image chicky_512.png that comes in the samples/data folder. Notice that this image is \(512 \times 512\), hence a downsample won't generate any error ( \(512 = 2^{9}\)). The original image is shown below:

First we apply two successive pyrDown() operations by pressing 'd'. Our output is:

Note that we should have lost some resolution due to the fact that we are diminishing the size of the image. This is evident after we apply pyrUp() twice (by pressing 'u'). Our output is now:
