Affine Transformations

Prev Tutorial: Remapping

Next Tutorial: Histogram Equalization

Goal

In this tutorial you will learn how to:

• Use the OpenCV function cv::warpAffine to implement simple remapping routines.
• Use the OpenCV function cv::getRotationMatrix2D to obtain a \(2 \times 3\) rotation matrix

Theory

What is an Affine Transformation?

1. A transformation that can be expressed in the form of a matrix multiplication (linear transformation) followed by a vector addition (translation).

2. From the above, we can use an Affine Transformation to express:

   1. Rotations (linear transformation)
   2. Translations (vector addition)
   3. Scale operations (linear transformation)

   you can see that, in essence, an Affine Transformation represents a relation between two images.

3. The usual way to represent an Affine Transformation is by using a \(2 \times 3\) matrix.

   \[ A = \begin{bmatrix} a_{00} & a_{01} \\ a_{10} & a_{11} \end{bmatrix}_{2 \times 2} B = \begin{bmatrix} b_{00} \\ b_{10} \end{bmatrix}_{2 \times 1} \]

   \[ M = \begin{bmatrix} A & B \end{bmatrix} = \begin{bmatrix} a_{00} & a_{01} & b_{00} \\ a_{10} & a_{11} & b_{10} \end{bmatrix}_{2 \times 3} \]

   Considering that we want to transform a 2D vector \(X = \begin{bmatrix}x \\ y\end{bmatrix}\) by using \(A\) and \(B\), we can do the same with:

   \(T = A \cdot \begin{bmatrix}x \\ y\end{bmatrix} + B\) or \(T = M \cdot [x, y, 1]^{T}\)

   \[T = \begin{bmatrix} a_{00}x + a_{01}y + b_{00} \\ a_{10}x + a_{11}y + b_{10} \end{bmatrix}\]

How do we get an Affine Transformation?

1. We mentioned that an Affine Transformation is basically a relation between two images. The information about this relation can come, roughly, in two ways:
   1. We know both \(X\) and T and we also know that they are related. Then our task is to find \(M\)
   2. We know \(M\) and \(X\). To obtain \(T\) we only need to apply \(T = M \cdot X\). Our information for \(M\) may be explicit (i.e. have the 2-by-3 matrix) or it can come as a geometric relation between points.

2. Let's explain this in a better way (b). Since \(M\) relates 2 images, we can analyze the simplest case in which it relates three points in both images. Look at the figure below:

   

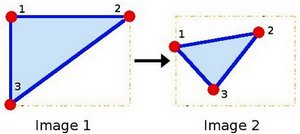
   the points 1, 2 and 3 (forming a triangle in image 1) are mapped into image 2, still forming a triangle, but now they have changed notoriously. If we find the Affine Transformation with these 3 points (you can choose them as you like), then we can apply this found relation to all the pixels in an image.

Code

• What does this program do?
  • Loads an image
  • Applies an Affine Transform to the image. This transform is obtained from the relation between three points. We use the function cv::warpAffine for that purpose.
  • Applies a Rotation to the image after being transformed. This rotation is with respect to the image center
  • Waits until the user exits the program

C++

• The tutorial's code is shown below. You can also download it here

  
  #include "opencv2/imgcodecs.hpp"
  #include "opencv2/highgui.hpp"
  #include "opencv2/imgproc.hpp"
  #include <iostream>
  
  using namespace cv;
  using namespace std;
  
  int main( int argc, char** argv )
  {
      CommandLineParser parser( argc, argv, "{@input | ../data/lena.jpg | input image}" );
      Mat src = imread( parser.get<String>( "@input" ) );
      if( src.empty() )
      {
          cout << "Could not open or find the image!\n" << endl;
          cout << "Usage: " << argv[0] << " <Input image>" << endl;
          return -1;
      }
  
      Point2f srcTri[3];
      srcTri[0] = Point2f( 0.f, 0.f );
      srcTri[1] = Point2f( src.cols - 1.f, 0.f );
      srcTri[2] = Point2f( 0.f, src.rows - 1.f );
  
      Point2f dstTri[3];
      dstTri[0] = Point2f( 0.f, src.rows*0.33f );
      dstTri[1] = Point2f( src.cols*0.85f, src.rows*0.25f );
      dstTri[2] = Point2f( src.cols*0.15f, src.rows*0.7f );
  
      Mat warp_mat = getAffineTransform( srcTri, dstTri );
  
      Mat warp_dst = Mat::zeros( src.rows, src.cols, src.type() );
  
      warpAffine( src, warp_dst, warp_mat, warp_dst.size() );
  
      Point center = Point( warp_dst.cols/2, warp_dst.rows/2 );
      double angle = -50.0;
      double scale = 0.6;
  
      Mat rot_mat = getRotationMatrix2D( center, angle, scale );
  
      Mat warp_rotate_dst;
      warpAffine( warp_dst, warp_rotate_dst, rot_mat, warp_dst.size() );
  
      imshow( "Source image", src );
      imshow( "Warp", warp_dst );
      imshow( "Warp + Rotate", warp_rotate_dst );
  
      waitKey();
  
      return 0;
  }

Java

• The tutorial's code is shown below. You can also download it here

  import org.opencv.core.Core;
  import org.opencv.core.Mat;
  import org.opencv.core.MatOfPoint2f;
  import org.opencv.core.Point;
  import org.opencv.highgui.HighGui;
  import org.opencv.imgcodecs.Imgcodecs;
  import org.opencv.imgproc.Imgproc;
  
  class GeometricTransforms {
      public void run(String[] args) {
          String filename = args.length > 0 ? args[0] : "../data/lena.jpg";
          Mat src = Imgcodecs.imread(filename);
          if (src.empty()) {
              System.err.println("Cannot read image: " + filename);
              System.exit(0);
          }
  
          Point[] srcTri = new Point[3];
          srcTri[0] = new Point( 0, 0 );
          srcTri[1] = new Point( src.cols() - 1, 0 );
          srcTri[2] = new Point( 0, src.rows() - 1 );
  
          Point[] dstTri = new Point[3];
          dstTri[0] = new Point( 0, src.rows()*0.33 );
          dstTri[1] = new Point( src.cols()*0.85, src.rows()*0.25 );
          dstTri[2] = new Point( src.cols()*0.15, src.rows()*0.7 );
  
          Mat warpMat = Imgproc.getAffineTransform( new MatOfPoint2f(srcTri), new MatOfPoint2f(dstTri) );
  
          Mat warpDst = Mat.zeros( src.rows(), src.cols(), src.type() );
  
          Imgproc.warpAffine( src, warpDst, warpMat, warpDst.size() );
  
          Point center = new Point(warpDst.cols() / 2, warpDst.rows() / 2);
          double angle = -50.0;
          double scale = 0.6;
  
          Mat rotMat = Imgproc.getRotationMatrix2D( center, angle, scale );
  
          Mat warpRotateDst = new Mat();
          Imgproc.warpAffine( warpDst, warpRotateDst, rotMat, warpDst.size() );
  
          HighGui.imshow( "Source image", src );
          HighGui.imshow( "Warp", warpDst );
          HighGui.imshow( "Warp + Rotate", warpRotateDst );
  
          HighGui.waitKey(0);
  
          System.exit(0);
      }
  }
  
  public class GeometricTransformsDemo {
      public static void main(String[] args) {
          // Load the native OpenCV library
          System.loadLibrary(Core.NATIVE_LIBRARY_NAME);
  
          new GeometricTransforms().run(args);
      }
  }

Python

• The tutorial's code is shown below. You can also download it here

  from __future__ import print_function
  import cv2 as cv
  import numpy as np
  import argparse
  
  
  parser = argparse.ArgumentParser(description='Code for Affine Transformations tutorial.')
  parser.add_argument('--input', help='Path to input image.', default='lena.jpg')
  args = parser.parse_args()
  
  src = cv.imread(cv.samples.findFile(args.input))
  if src is None:
      print('Could not open or find the image:', args.input)
      exit(0)
  
  
  
  srcTri = np.array( [[0, 0], [src.shape[1] - 1, 0], [0, src.shape[0] - 1]] ).astype(np.float32)
  dstTri = np.array( [[0, src.shape[1]*0.33], [src.shape[1]*0.85, src.shape[0]*0.25], [src.shape[1]*0.15, src.shape[0]*0.7]] ).astype(np.float32)
  
  
  
  warp_mat = cv.getAffineTransform(srcTri, dstTri)
  
  
  
  warp_dst = cv.warpAffine(src, warp_mat, (src.shape[1], src.shape[0]))
  
  
  # Rotating the image after Warp
  
  
  center = (warp_dst.shape[1]//2, warp_dst.shape[0]//2)
  angle = -50
  scale = 0.6
  
  
  
  rot_mat = cv.getRotationMatrix2D( center, angle, scale )
  
  
  
  warp_rotate_dst = cv.warpAffine(warp_dst, rot_mat, (warp_dst.shape[1], warp_dst.shape[0]))
  
  
  
  cv.imshow('Source image', src)
  cv.imshow('Warp', warp_dst)
  cv.imshow('Warp + Rotate', warp_rotate_dst)
  
  
  
  cv.waitKey()
  

Explanation

• Load an image:

C++

    CommandLineParser parser( argc, argv, "{@input | ../data/lena.jpg | input image}" );
    Mat src = imread( parser.get<String>( "@input" ) );
    if( src.empty() )
    {
        cout << "Could not open or find the image!\n" << endl;
        cout << "Usage: " << argv[0] << " <Input image>" << endl;
        return -1;
    }

Java

        String filename = args.length > 0 ? args[0] : "../data/lena.jpg";
        Mat src = Imgcodecs.imread(filename);
        if (src.empty()) {
            System.err.println("Cannot read image: " + filename);
            System.exit(0);
        }

Python

parser = argparse.ArgumentParser(description='Code for Affine Transformations tutorial.')
parser.add_argument('--input', help='Path to input image.', default='lena.jpg')
args = parser.parse_args()

src = cv.imread(cv.samples.findFile(args.input))
if src is None:
    print('Could not open or find the image:', args.input)
    exit(0)

• Affine Transform: As we explained in lines above, we need two sets of 3 points to derive the affine transform relation. Have a look:

C++

    Point2f srcTri[3];
    srcTri[0] = Point2f( 0.f, 0.f );
    srcTri[1] = Point2f( src.cols - 1.f, 0.f );
    srcTri[2] = Point2f( 0.f, src.rows - 1.f );

    Point2f dstTri[3];
    dstTri[0] = Point2f( 0.f, src.rows*0.33f );
    dstTri[1] = Point2f( src.cols*0.85f, src.rows*0.25f );
    dstTri[2] = Point2f( src.cols*0.15f, src.rows*0.7f );

Java

        Point[] srcTri = new Point[3];
        srcTri[0] = new Point( 0, 0 );
        srcTri[1] = new Point( src.cols() - 1, 0 );
        srcTri[2] = new Point( 0, src.rows() - 1 );

        Point[] dstTri = new Point[3];
        dstTri[0] = new Point( 0, src.rows()*0.33 );
        dstTri[1] = new Point( src.cols()*0.85, src.rows()*0.25 );
        dstTri[2] = new Point( src.cols()*0.15, src.rows()*0.7 );

Python

srcTri = np.array( [[0, 0], [src.shape[1] - 1, 0], [0, src.shape[0] - 1]] ).astype(np.float32)
dstTri = np.array( [[0, src.shape[1]*0.33], [src.shape[1]*0.85, src.shape[0]*0.25], [src.shape[1]*0.15, src.shape[0]*0.7]] ).astype(np.float32)

You may want to draw these points to get a better idea on how they change. Their locations are approximately the same as the ones depicted in the example figure (in the Theory section). You may note that the size and orientation of the triangle defined by the 3 points change.

• Armed with both sets of points, we calculate the Affine Transform by using OpenCV function cv::getAffineTransform :

C++

    Mat warp_mat = getAffineTransform( srcTri, dstTri );

Java

        Mat warpMat = Imgproc.getAffineTransform( new MatOfPoint2f(srcTri), new MatOfPoint2f(dstTri) );

Python

warp_mat = cv.getAffineTransform(srcTri, dstTri)

We get a \(2 \times 3\) matrix as an output (in this case warp_mat)

• We then apply the Affine Transform just found to the src image

C++

    Mat warp_dst = Mat::zeros( src.rows, src.cols, src.type() );

    warpAffine( src, warp_dst, warp_mat, warp_dst.size() );

Java

        Mat warpDst = Mat.zeros( src.rows(), src.cols(), src.type() );

        Imgproc.warpAffine( src, warpDst, warpMat, warpDst.size() );

Python

warp_dst = cv.warpAffine(src, warp_mat, (src.shape[1], src.shape[0]))

with the following arguments:

• src: Input image
• warp_dst: Output image
• warp_mat: Affine transform
• warp_dst.size(): The desired size of the output image

We just got our first transformed image! We will display it in one bit. Before that, we also want to rotate it...

• Rotate: To rotate an image, we need to know two things:

  1. The center with respect to which the image will rotate
  2. The angle to be rotated. In OpenCV a positive angle is counter-clockwise
  3. Optional: A scale factor

  We define these parameters with the following snippet:

C++

    Point center = Point( warp_dst.cols/2, warp_dst.rows/2 );
    double angle = -50.0;
    double scale = 0.6;

Java

        Point center = new Point(warpDst.cols() / 2, warpDst.rows() / 2);
        double angle = -50.0;
        double scale = 0.6;

Python

center = (warp_dst.shape[1]//2, warp_dst.shape[0]//2)
angle = -50
scale = 0.6

• We generate the rotation matrix with the OpenCV function cv::getRotationMatrix2D , which returns a \(2 \times 3\) matrix (in this case rot_mat)

C++

    Mat rot_mat = getRotationMatrix2D( center, angle, scale );

Java

        Mat rotMat = Imgproc.getRotationMatrix2D( center, angle, scale );

Python

rot_mat = cv.getRotationMatrix2D( center, angle, scale )

• We now apply the found rotation to the output of our previous Transformation:

C++

    Mat warp_rotate_dst;
    warpAffine( warp_dst, warp_rotate_dst, rot_mat, warp_dst.size() );

Java

        Mat warpRotateDst = new Mat();
        Imgproc.warpAffine( warpDst, warpRotateDst, rotMat, warpDst.size() );

Python

warp_rotate_dst = cv.warpAffine(warp_dst, rot_mat, (warp_dst.shape[1], warp_dst.shape[0]))

• Finally, we display our results in two windows plus the original image for good measure:

C++

    imshow( "Source image", src );
    imshow( "Warp", warp_dst );
    imshow( "Warp + Rotate", warp_rotate_dst );

Java

        HighGui.imshow( "Source image", src );
        HighGui.imshow( "Warp", warpDst );
        HighGui.imshow( "Warp + Rotate", warpRotateDst );

Python

cv.imshow('Source image', src)
cv.imshow('Warp', warp_dst)
cv.imshow('Warp + Rotate', warp_rotate_dst)

• We just have to wait until the user exits the program

C++

    waitKey();

Java

        HighGui.waitKey(0);

Python

cv.waitKey()

Result

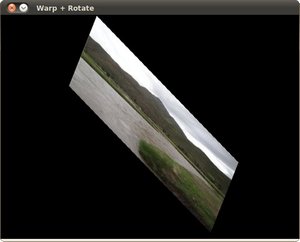
• After compiling the code above, we can give it the path of an image as argument. For instance, for a picture like:

  

  after applying the first Affine Transform we obtain:

  

  and finally, after applying a negative rotation (remember negative means clockwise) and a scale factor, we get: